作者 | 张英伯 (北京师范大学数学科学学院),文志英(清华大学数学科学系)
来源 | 《数学通报》2013年 第52卷 第一期,原载《数学文化》2012年第3卷第4期
在大学数学系里教书,经常看到和听到与法国有关的事情。主要是他们的数学如何厉害,像笛卡尔、伽罗瓦、庞加菜、嘉当这些在数学史上振聋发聩的名字就不用说了,仅就上世纪中叶开始颁发的菲尔兹奖而言,美国有15位获奖人、法国11人、俄罗斯(包括前苏联)8人、英国6人、日本3人、比利时2人,欧洲和澳洲的一些国家,包括德国各1人,共52人。美籍获奖者有5人来自欧亚两洲,法籍有2人,分别来自德国和越南。有趣的是,法裔的获奖者全部都在法国,好像这里的环境非常适合数学家的生存。1994年法国有两人获奖,2002、2006年各一人,2010年两人。2002年的世界数学家大会是在北京召开的,会议期间,北师大还邀请世界各地的数学家到京师大厦晚宴,当年的菲尔兹奖得主 Laurent Lafforgue 也来了。我们有一些熟悉的德国代数界的同事,在本国没有找到位置,去了法国,他们说法国政府吸引欧洲、拉丁美洲一些有成就的数学家来到法国任教,中国也有三十多位数学家在那里找到了教职,其中以数学著称的巴黎六大、七大和十一大各有一人。2009年初,法国教育部有一位数学督察访问北师大,谈到了法国数学教师的培养和选拔,还给了一份法国一般方向科学系列数学课程第三学年的课程纲要,水平果然不凡。[1,2]
法国的人口约为六千五百万,是美国的22%,中国的5%,他们的教育是怎样搞的?他们的数学成就何以会如此出色?
出类拔萃的中学
请示了中国数学会,首师大李克正、李庆忠教授,北师大二附中金宝铮、实验中学姚玉平两位特级教师,北师大王昆扬、张英伯教授共6人于2012年5月27日来到巴黎考察数学教育。
第二天一早差五分七点,我们到达旅馆大堂,按照约定的时间七点去拜会巴黎七大的 Michele Artigue 教授。Michele 曾经担任过国际数学教育委员会(ICMI)的主席,去年年初在北京师范大学召开的 ICMI 执委会的会议上,担任本届执委的张英伯与她谈到中国的数学教授和数学老师想了解法国数学教育的愿望,这次访问就是她安排的。没想到 Michele 早就到了大堂,已经等我们十分钟了。按照法国的礼节拥抱问候完毕,她立刻带领我们动身前往此次访问的第一个学校:路易大帝中学,这是法国最顶尖的一所学校,只设高中和预科,不设初中。
路易大帝中学是公办学校,拥有选择学生入学的权利,选择的方式是按照各校初中生的学习档案和成绩,由学校拍板录取,没有入学考试。主要生源为市中心地区的初中,这里集中了文化与经济水平较高的家庭。为了阻止名校变成“贵族学校”的趋向而引起社会的不公和不满,巴黎学区决定高水平的中学有强制性义务去发现郊区的优秀初中生,学区会特别观察这类学生从高一到大学的整个历程。于是负有此项社会义务的中学与一些较差地区的初中建立了特别的关系,派老师每周去给这些选拔出来的优秀初中生上补习课,为他们来市中心的学校顺利学习做准备,这些课程都是义务的,学校和老师分文不取,应该指出的是,法国初中数学纲要的原则是提出对学生的最低要求,如果老师认为学生在认知上能够接受就可以超过纲要讲得更深一些。
法国各省都有这类优秀的高中。与世界上其他国家不同的是,这类高中开设两年制的大学预科,学习大学本科课程,而大学一年级的微积分和向量已经在高三学完了[2]。学生高中毕业经过严格的挑选进入预科,毕业后可以报考法国的大学校。法国高中毕业有统一的会考,发放毕业证书。进入一般的大学没有入学考试,报名即可,但是大学校各自的入学考试题却严格、高深得令人惊叹。
我们进入学校大门时,路易大帝中学的副校长和几位负责的老师已经站成一排在门口等候,寒暄了几句,我们被领着参观了学校的全貌。学校位于巴黎拉丁区的中心,已经有450年的历史,目前的校园是200年前建造的,在上世纪中期和末期进行过翻修。教学楼都是四层的,建筑风格与巴黎城一致。校园有四个由若干座教学楼围成的院子,一所钟楼和教堂,其中两个院子以校友的名字冠名,分别叫做雨果院和莫里哀院。如果不是看到课间休息时院子里生龙活虎的现代派的孩子们,单就建筑风格而言,你会觉得走进了雨果笔下十九世纪的法兰西。

法国的预科一般分成文、理、商三科,各自按照法国大学第一阶段(即大学第一、二年)的课程纲要授课。法国的纲要是针对课程内容的最低要求给出的指导性意见,弹性很大,各校可以根据学生和师资水平因材施教,路易大帝中学的授课内容要远远多于和深于纲要。预科也没有统一的课本,课本由老师自行选择,或者自己编写讲义;考试也都是老师自己出题,自己判卷,从来没有统考。
自上世纪70年代至90年代中,理工科预科一般用 Jacques Dixmie r的《第一阶段数学教程》,至今一些著名的预科班仍然以此为蓝本,武大“中法班”从1980年至1990年也一直在用。仅从教材的目录,对其深度和广度就可窥见一斑。教材的出台还有一段背景:在上世纪60年代的西欧,法国几何学家埃里·嘉当(Elie Cartan)的儿子亨利·嘉当(Henry Cartan)领衔发起了高等数学教学的一场改革,摒弃了十九世纪以来一些陈旧的内容,适应现代需要,从教材的整体结构上给予更新,一方面增加了不少新的内容,另一方面用新的观点和视角去介绍传统的内容,强调了不同学科之间的联系。法国大学的数学纲要也适应了这一背景。稍后苏联亦更新了传统的菲赫金格尔茨的数学分析,代之以佐里奇的新课本。
路易大帝中学共有约 1800 名学生,850名高中生,22个班级,每班35-40人;950名预科生,20个班级,每班 40-45 人,约 350名学生住校。预科当中以理科为主,占60%;文科25%;商科15%。其中理科又分为数学物理工程班,每年级有4个班;物理化学工程班,每年级有2个班;文科和商科每年级各2个班。

在欧洲的中学进教室听课不太容易,校方无权命令老师接待来宾,需要和任课老师沟通协商。托 Michele Artigue 教授的福,我们得以进入预科的教室。遗憾的是我们来的时间不对,赶上期末复习考试,没有正课了,听的第一节课是工科的数学分析复习。当副校长把我们领进教室,全体孩子起立欢迎。我对教室的第一个印象是三面白墙到底,没有一幅图画或板报,也没有多媒体,如果将一面墙上的现代化绿色大黑板换成一块木质的老黑板,你会觉得雨果或者伽罗瓦在这里上课也很协调。Jerome Degot 老师四十岁左右,笑眯眯的,我们看不懂法文,但是看得出来板书规范。学生手里有老师编的复习题,已经都做过了,课上对一些较难的题目进行讨论,内容是定积分和不定积分。孩子们交头接耳,十分活跃,每当老师写下一道题目,至少有十个孩子高高举手,并不断地提出问题。孩子们的板书不太规范,却很认真,演算之外还不时地画图进行几何解释。
Michèle Artigue 教授告诉我们,为了更好地了解学生,因材施教,预科的数学老师要在两年的时间全程跟随学生,师生关系融洽。同一个老师需要教数学分析、线性代数、抽象代数、常微偏微、实变复变、数论、几何学、拓扑学等大学一、二年级的所有课程,而且课程进度比我们的大学数学系要快,部分内容要深,我们一下子被震住了,这就意味着,预科的老师要对现代数学的全部基础知识了如指掌,独当一面,自主性极强,我们当中有人教了一辈子代数或一辈子分析,还从来没有互换过角色。
路易大帝中学每堂课 55分钟,课间休息5分钟。我们听的第二堂课是商科的数学分析。教室后面有一张不大的世界地图,黑板上方正中贴了一幅威廉王子和凯特王妃的小照,看来法国孩子也挺喜欢英国王室啊。Jérome Gartner 老师是一位不到三十岁的小伙子,非常文静,讲课时显出些许腼腆。Michele说他刚从高师毕业,来这里试教。这堂课的内容是用 ε-δ 语言复习函数的极限,举了一个二元连续函数的例子,老师在黑板上画出 ε 在直线上的取值区间和对应的 δ 的平面上的取值区间,图形漂亮,公式清晰。课堂相当安静,学生没有课本,都在飞快地记笔记,十分整齐流利。让人觉得严格的数学推导与法国姑娘的美貌不大相宜。下课之后,我们就这节课对 Michele 表达了由衷地赞赏,她笑笑说,这是路易大帝中学的一般水平,今天没有机会进入最高水平的课堂。
午饭时间到了,孩子们排成长龙,叽叽喳喳愉快地等待进入食堂,校方招待我们在食堂的包间用餐。下午听了10年级(相当于我们的高一)的三角函数复习,由一位三十多岁,棕发披肩的女老师任课。可能因为孩子小,老师和学生都极其活跃,老师不停地发出“嘘嘘”声维持秩序。复习的内容不少,有两角和与两角差的公式、倍角公式以及公式的推导,然后参观了学校的物理实验室,有激光、机器人等等,实验室显不出一点富丽堂皇,反而有点像几十年前我们在中学读书时的样子,但是就从这些实验室里,很多学生进入了闻名世界的巴黎综合理工学院(Ecole Polytechnique de Paris)。

在路易大帝中学最生动有趣的节目当属参观图书馆。图书管理员 Agnès Franck 是一位身材丰满、精神矍铄的银发女士,提起自己的学校,脸上洋溢着无限的骄傲与自豪。法兰西有过辉煌的历史和文化,有过拿破仑时代对世界的征服,有过欧洲贵族以讲法语为高雅的年代,法国人的自豪和骄傲是可以理解的。Agnès Franck 告诉我们,在国家的高中毕业会考中,路易大帝中学的合格率为99%左右,其中三分之一能够留在本校的预科班;学校百分之百的预科毕业生能够考取高等学校,其中至少三分之一考入著名的巴黎综合理工学院,而该校每年有四分之一入校生来自路易大帝中学的预科。网上的统计数字显示,在2006年,巴黎高等师范学校数学物理科入学考试的第1,2,3,8,9名,数学物理信息科的第1名(中国学生),和物理化学工程科的第1,3,4,7,11名;巴黎综合理工学院的数学物理工程、物理化学工程,物理工程的三科状元;巴黎国家高等矿业学院的三科状元均出自路易大帝中学。
Agnès Franck 指给我们看图书馆里十九世纪的硬木书柜,书柜中有他们的校友——哲学家伏尔泰的全集。接着又拿出一本1588年法国王后凯瑟琳·德·美第奇(她原来是一位意大利公主)组织出版的书,书中介绍了意大利的历史和文化,使用了丝绸做成的纸张和特殊的油墨,用手指一弹,发出清脆的金属般的声响,永远不会褪色。意大利文艺复兴时代的繁荣,真是名不虚传呀!

Agnès Franck 说学校是路易十四建立的(应该是一些教士建立,路易十四支持的),他是法国历史上很有作为的一位国王。路易大帝中学的命运随着法国近代史上的政治动荡而历经磨难,在路易十五时代再一次得到皇家的支持,学校的印章刻上了皇家的旗帜(天蓝色背景下的三朵金百合花);学校大门刻上了路易十四和路易十五的雕像。她问我们是否知道罗伯斯庇尔,我们当然知道,那是法国大革命时期的革命领袖,中国的历史课本上必写的。她告诉我们罗伯斯庇尔是路易十六时代这个学校的学生。1775年,在一个下大雨的天气,路易十六坐马车来学校视察,老师和学生们站在雨地里夹道欢迎。因为罗伯斯庇尔书读得好,又乖巧听话,校方让他做代表致欢迎词。他讲得很漂亮,盛赞国王的英明。十八年后,他鼓动国民公会把这位“英明的国王”送上了断头台。
从图书馆出来,路易大帝中学一位曾在北京语言大学学习了三年的数学老师 Rémi Anicotte 陪我们继续参观。这位老师的中文就像我们一样流利,看上去非常机敏,他的中文名字叫安立明。路易大帝中学从高一到高三都有欧洲班(历史和地理课程特殊、英语加强),还有一个东方班,每周有一小时的中文数学课。当我们走进学校的小教堂时,安老师告诉我们其实伏尔泰不是路易大帝中学的毕业生,那个年代资源紧缺,每年冬初神父都在教堂放一小盆圣水,圣水什么时候结冰,学校什么时候给学生升火。有一年很冷,伏尔泰看到教堂的圣水总是不结冰,就偷偷去河里取来一块冰放进了圣水盆中。事情被发现了,神父大怒,伏尔泰被开除。安老师笑笑说,这件事不是伏尔泰的耻辱,而是学校的耻辱。我们问是不是因为这个,学校里没有伏尔泰院。
学校正门内的大厅中有一个小小的玻璃柜,里面陈列着从路易大帝中学毕业的数学家。其中有伽罗瓦、刘维尔、厄米特、阿达玛、勒贝格、波莱尔、达布等17位,10位有肖像或照片,伽罗瓦的像特别可爱,20多岁决斗身亡的他在一群表情严肃的数学家之间活脱一个小娃娃。安老师开玩笑说,幸亏学校当年没有开除伽罗瓦,否则这个玻璃柜里就无权摆上他的肖像;学校也没有伽罗瓦院,因为数学不像小说戏剧那样广为民众所知。
从路易大帝中学走过一条街,就看到了圆顶的法国先贤祠矗立在一个小高坡上,伏尔泰、雨果、皮埃尔·居里、玛丽·居里、卢梭等等为法兰西和世界的科学文化做出过杰出贡献的人们安息在这里。学校周围还有索邦大学、法兰西学院等著名的建筑,充满了学术氛围。

Michèle Artigue 教授还带我们去了巴黎东郊 Vincennes 市的 Hector Berlioz 中学,这也是一所不错的学校,具有招收预科班的资质,高中毕业国家会考的通过率在90%。这里的每节课也是55分钟,课间休息5分钟。我们在这天下午连续听了同一个老师的三节课,再一次领教了法国中学教师的数学功底。Rhydwen Volsik 老师高高的个子,朴实而内敛。他每周上17节课,教三个正常班,5个兴趣班:兴趣班包括10年级的图论,11年级的概率论,12年级的群论。第一节是10年级正常班的三角函数复习,第二节是12年级兴趣小组的群论,有五个男孩儿,三个女孩儿,因为这几个孩子准备高中毕业后去英语国家留学,老师用英语授课,并发给学生和我们每人一份他编写的英文讲义 An Introduction to Group Theory,我们终于能够听懂整节课,不用看着公式猜了,这节课的内容是群的定义,孩子们争着到黑板上证明诸如等边三角形的对称变换为什么构成一个群,而非零有理数的除法为什么不能构成一个群之类的问题。第三节是10年级兴趣小组的图论,不到10个学生,仍然发讲义,讲英语,不是一般性的介绍,而是严格的定义和推导,小小的孩子们看来是听懂了,课堂上仍然异常活跃。
特别搞笑的是,下课后我们打算在校门口拍照留念,绕校园一周竟然找不到我们心目中一所重点中学应该有的排场漂亮的大门。直到 Michele Artigue 和学校的老师谈完事情出来,才告诉我们进入学校大楼的铁栅栏门旁有一个牌子,那就是学校的标志。
制度化的英才教育
Michele Artigue毕业于巴高师,在七大数学系工作,多年来讲授数学分析。她组织并领导了系内一个数学教育研究所(IRME),研究所的成员有几位七大的老师,半天在系里上课,半天在研究所,或者四分之三时间搞数学,四分之一在研究所;还有十几位巴黎市内各地区的数学督查,二十几位中学数学老师。我们问其他大学有没有这样的研究所,她说极少,也没有全职从事数学教育研究的教授,最多半职,但是社区大学有全职从事这方面工作的老师。

Michèle Artigue特别敬业,她领我们去学校或者研究所访问,从来都是健步如飞,我们当中比她年轻二十岁的老师都不大跟得上趟。作者与她在执委会共事三年,经常通过 ICMI 的电子邮件交流得知她在世界各地的发展中国家飞来飞去,如非洲、拉丁美洲,在一些条件特别艰苦的国家和地区举办教师培训班,组织各种活动,有时甚至在那里滞留一个多月。最近她又发起了一个克莱因(Klein)项目,请数学家们撰写短小的科普文章,帮助中学老师了解数学的最新动态。如果吉尼斯要评选最诚恳、最敬业、最勤奋的人,Michele Artigue 应当是一个合适的人选。在我们离开之后的一周,世界各地的数学教育工作者来到巴黎,为她的光荣退休举行了纪念会,我们未能出席,请出席会议的中国老师转达了我们的感谢和敬意。
在巴黎七大与 IREM 的老师座谈时,他们不理解并感到惊讶的一点是:中国的数学基础教育那么出色,国际奥林匹克竞赛连年第一,国际上针对中学数学课堂的各种测试从来名列前茅,你们这几个人为什么要来法国考察数学基础教育呢?
应 Michele Artigue 的邀请,张英伯和李庆忠联名在他们的讨论班上做了一个《中国数学教育的传统》(Tradition of Chinese Mathematical Education)的报告,介绍了中国数学教育的历史和现状。我们五千年的文明古国是一个非常重视教育的国家。在渔猎和农耕时代,中国的生产力名列世界前茅。当然从工业时代开始中国就没有跟上世界前进的脚步,但是清末民初以来,我们逐步发展了民族工业,引入了世界通行的学校教育。1949年之后,我国教育的基本特点是高度统一:统一管理,统一大纲(或课标),统一课本,统一考试。改革开放后课本有所松动,考试改为各省命题,但全国的中小学仍然在统一课标的指导下齐步前进。在大多数国家作为最低标准的课标,在我们这里却是上下均不可超越的绝对标准。
在我国与国际社会隔绝的上世纪49-78年,这种体制培养了一批国防工业和其它领域亟需的科技人才。改革开放之后,这种体制使得我们的学校总体水平高于发达国家的一般中小学,使得我们可以倾全国之力,像培养参加奥林匹克运动会的运动健将那样,选拔和训练数学出色的中学生去参加国际奥林匹克数学竞赛,并连年高居榜首。但这却无法产生引领科学技术发展的大科学家。西方国家的数学基础教育有很多弊病,特别是过度的去数学化倾向,但是他们十分重视英才教育,因而可以培养出最优秀的人才去引领科技发展,去治理企业和国家。事实上,孩子们的天赋和才能表现在各个不同的方面,差异是非常大的,这就像在体育课上让学生们跳高,假设有5%的孩子能够跳过一米八,95%的孩子只能跳过一米二,如果标杆一定要固定在一米五不许改变,那么很多孩子因跳不过去而丧失了信心,少数有天赋的孩子因无法继续提高而丧失了成为运动健将的可能。
当得知我们的国际奥林匹克数学竞赛金银铜牌得主大部分没有继续学习数学,而是选择了大学的其它院系,学了数学的也只有少数人在从事数学研究;我们同一个区县的所有中小学里所有的学生,无论喜欢数学与否都用同样的数学课本,所有的初中生都参加市或区县统一的高中入学考试(简称中考);同一个省或直辖市的所有高中毕业生都参加统一的高等院校入学考试,所有的高等院校都按照统考成绩统一录取学生时,IREM的老师也很惊讶,难以理解这种官方对学校的严格控制是如何操作的。看来是不同的政治体制造就了不同的教育制度,互相理解起来还真有点儿费劲。
在IREM的讨论班上,2009年春天访问过北师大的教育部数学督察也来了,我们高兴地握手问候。记得他那时候说过,中国学生的数学基础水平比欧洲国家要高,比法国德国高两年,比意大利高三年。
法国的小学(5年制,6-11 岁)和初中(4年制,11-15岁)课程纲要对全国学生的要求是一致的,但是学生从高中开始分流,40%进入两年的职业教育,称为 Professional,毕业后使学生具有最低的工作技能,但仍然有机会进大学深造。这部分学校又分成三类:
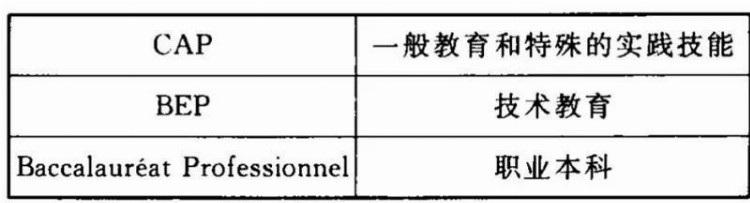
数学课的周学时分别为1.5-2,2-3,和2学时。课程内容差别很大,视专业而定,比如有平面和空间几何、三角函数、方程和不等式、指数和对数、金融数学基础、经营数学,也有一些微积分初步等等。
60%的学生进入高中(三年制,15-18岁),头一年是所谓的“判断阶段”(cycle dedetermination),学习相同的课程;后两年是所谓的“结业阶段”(cycle terminal)在老师的指导下分科。这部份分为一般方向和技术方向,其中一般方向包括三个系列:
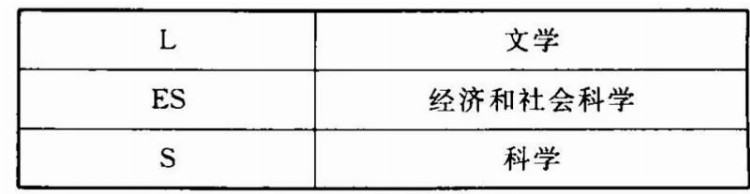
而技术方向包括四个系列:
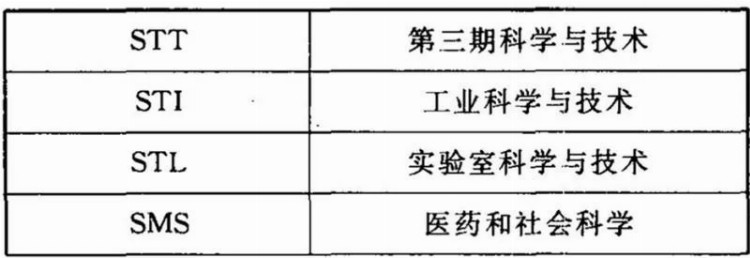
其中一般方向科学系列的12年级(高三)课程纲要已由北京师范大学数学系留法教授邓冠铁译成中文了,内容有复数、微分、积分、向量,相当于工科大学一年级的数学水平[2]。法督所言我们的数学基础水平比别国高,当指小学和初中。
我们很长时间搞不明白中国小学和初中的数学为什么会比欧美国家强,这些课程不是我们从十九世纪末二十世纪初开始向西方国家、五十年代后向前苏联学过来的吗?在2012年7月韩国举行的 ICMI 执委会上,有一次作者与意大利的执委 Mariolina Bartolini Bussi 一起乘出租车,她是搞小学数学教育研究的,为人真诚,谦和善良。意大利的小学数学被认为最差,Mariolina 曾感叹过多次,在车上她又一次谈到中国小学生的计算能力要比意大利强得太多。作者告诉她中国上世纪前半叶所用的数学课本都是从发达国家引进,或参照他们的课本编写的。她说在那个年代意大利小学生的计算能力也是很强的,这话肯定不假,因为她本人就是那个年代的小学生。这句话令人恍然大悟,我们在上世纪后半叶的很长时间里与国际社会脱节,始终不知道西方国家已经在实施大众教育,推行教育公平的过程中将数学大大地弱化了。我们将那时的课程保留了下来,现在还没有完全被弱化掉;加之我们中国老师的勤恳敬业,并且国家多年来在中小学数学教育中贯彻了重视“基础知识,基本技能”的双基原则,自然比别人强了。看来有一弊也可能会有一利,历史就是这样螺旋式上升的啊。
数学家的主导作用
Michele Artigue 还陪同我们访问了法国教育部,接待我们的是教育部国际司亚非科科长 Marc Melka 先生及其秘书,他们系统地为我们介绍了法国教育的全貌。他说法国每年有280万学生进入高等教育,高等教育分成两个部分:83所大学(Un
