
导语
1963年,洛伦兹用蝴蝶效应形象地展现出了混沌的魅力:亚马逊热带雨林中的一只蝴蝶偶尔扇动几下翅膀,可以在两周以后引起美国得克萨斯州的一场龙卷风。正所谓“失之毫厘,谬以千里”,混沌理论告诉我们,即使人类掌握了确定性规则,依旧无法拥有预测未来的能力。本文从混沌的天气预测实验开始,介绍了混沌理论和实例:从分岔到分形,从树木、血管这些自然界的实例,到量子混沌再到人类的意识。
关键词:混沌理论,分形,量子混沌,意识
Irfan Bashir, Hamid Rashid Shah | 作者
牛晓杰 | 译者
梁金 | 审校
邓一雪 | 编辑
目录
1. 一个混沌理论的实验
2. 解释混沌理论:混沌科学
3. 什么是混沌理论?
4. 混沌斑图
5. 混沌理论举例
6. 量子混沌
7. 混沌理论与意识
1. 一个混沌理论的实验
在60年前一个寒冷的冬天,爱德华·洛伦兹正在他的电脑上进行一个天气模式模拟的实验。在输入了一些数字之后,他出去喝了杯咖啡。等到他10分钟后再次回来的时候,发现一些古怪的结果。由此他发现了后来著名的混沌理论——一个将永远改变科学的发现!
他的电脑模型是12个变量的组合,每一个变量代表天气的一个方面,诸如温度和风速。洛伦兹当时正在重复他之前的模拟。然而,当洛伦兹把他程序里的变量从0.506127四舍五入成0.506时,未来两个月的整个天气预测模式都完全改变了。在正常参数下,给定相同的起点,天气每次都会以相同的模式展开。而给定一个稍微不同的起点,天气应该以稍微不同的模式展开。四舍五入造成的误差肯定是微不足道的,它不应该造成什么大规模的影响。
在那个时期,科学的假设是,只要了解物理定律和系统的初始条件,就可以计算出一个封闭系统的大致行为。科学思维是,另一个星球上树叶的掉落不会影响到地球上台球的运动。人们相信,小的变化不会造成大的影响。法国数学家皮埃尔-西蒙·拉普拉斯(Pierre-Simon Laplace)在1814年出版的《概率哲学论文》( )中说,如果我们知道宇宙目前的一切,那么“没有什么是不确定的,未来就像过去一样,会毫无保留的呈现在‘我们’眼前”。
但是,在洛伦兹的特殊微分方程系统中,随着时间的推移,小的错误会造成深不可测的变化。这些问题凝视着他,但他并没有答案。是否简单的模型可以产生显著的随机性?是否在一个系统中的简单模型会在另一个系统产生复杂性?是否随机性并不是模糊测量的副产品,而是一种常态?是否混沌并不是人类观察局限性的结果,而就是自然的底层法则?
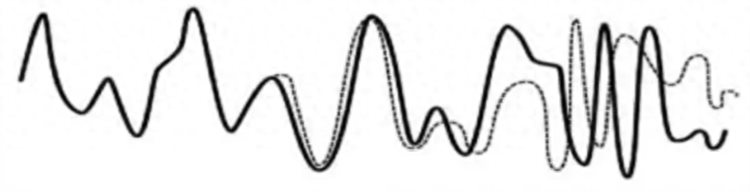
图.运行了两个月的两个模拟天气斑图
这个出乎意料的结果使洛伦兹意识到,小的改变可以造成大的影响——这是对自然运转方式的强有力洞察。这个想法被称为“蝴蝶效应”。混沌效应或者蝴蝶效应就是用来表述“小的改变导致整个混沌系统重大变化”的观点。蝴蝶效应这个术语是洛伦兹提出的,他假设一只远处的蝴蝶拍打翅膀的行为可以引起一系列的复杂事件,最终导致其他地方的一场龙卷风。洛伦兹意识到,对初始条件的敏感性是导致非周期性行为的原因。这种效应后来获得了一个专有名词:初始条件依赖敏感性。然而,看一下民间传说就会发现,古代的诗人已经知道并回答了什么是混沌理论:
“因为少了一颗马蹄钉,而丢了一个马蹄铁。
因为丢了一个马蹄铁,而少了一匹战马。
因为少了一匹战马,而缺了一个骑兵。
因为缺了一个骑兵,而输了一场战役。
因为输了一场战役,而灭亡了整个国家。”
2.解释混沌理论:混沌科学
正如詹姆斯·格雷克(James Gleick)在他的书《混沌》()中所说,“在混沌开始的地方,经典科学就止步了。只要世界上有物理学家在试图探究自然规律,TA就会在面对大气中的无序状态、动荡的海洋、野生动物种群的波动、心脏和大脑的振荡时感到特别的无知。自然界有其不规则、不连续和不稳定的一面。”
混沌科学孕育了自己的语言,包括分形、湍流、周期性、分岔、奇异吸引子、蝴蝶效应和敏感依赖等词汇。这些词代表了一个规则不同的世界——事物分支成奇怪的结构,遵循一种可以知道但不可能精确量化和预测的斑图和周期性。如果通过时空连续体的棱镜来参考,那么这个混沌世界的一切就好像是折回自身,同时成为未来和过去——它从自身汲取其周期性。混沌不是对秩序的拒绝,而是秩序的自然表达。
混沌科学似乎可以回答一些人类苦苦追寻的最基本问题。生命是如何开始的?什么是湍流?最重要的是,在一个创造更多无序的熵支配的宇宙中,秩序如何产生?以及古老的科学问题:微观世界如何将自己编织进宏观世界。孤立地研究一个原子或神经元时,其行为方式是一样的,但数十亿个原子和神经元的行为方式却完全不同。这是一门解开周期性和不可预测性之间联系的科学。
3.什么是混沌理论
混沌的核心是对非线性的研究,这意味着玩游戏的行为有可能改变规则本身。非线性使得对非线性事物的理解变得困难,因为不同变量之间存在错综复杂的变化性,从而创造了丰富而复杂的行为。例如,人们不能给摩擦力定义一个恒定的重要性,因为它的重要性取决于速度,而速度又取决于摩擦力。因此,量化非线性就像解一个魔方,每次移动它时颜色都会改变。
让我们考虑一些最常见的日常例子:
3.1 预测天气
过去两个世纪技术发生了重大变革,短期内的天气预测水平已经大大提升。但是长期天气预测仍然是棘手的问题。大部分现代天气预测模型,甚至是人工智能驱动的模型,都是通过分布在10-200公里范围内的地理监测点的网格进行预测。为了确定天气,气象学家使用一系列微分方程来分析原始数据,其中包括露水强度、温度、风、压力以及其他变量。但是地面站和卫星不能观察到所有的东西,因此对于一些起始数据,例如水分,必须通过猜测给定数值。大多数情况下,这种猜测是可靠的。
但是,假设我们能够将设备升级到足够精确的水平,并且用间隔仅几英尺的传感器覆盖整个地球;假设每个传感器都能给出气象学家想要观察的完全准确的读数;假设一台由人工智能驱动的量子计算机能够接收所有这些读数,并计算出以分钟为间隔的天气模式。那会发生什么?如果以上所有假设成立,我们是否能够绝对准确地预测天气?
我们将观察到的是,我们仍然无法预测特定地点或长期的天气模式。传感器之间的空间将隐藏微观波动——它一直延伸到量子范围,但是计算机并不知道。这些其实只是相比于平均水平的微小偏差。但在几分钟内,这些波动已经在几英尺外造成了微小的错误。很快,乘数效应(Multiplier Effect)将随之而来,错误将累计,甚至会扩展到10英尺的距离范围。因此,这使得人们不可能绝对准确地预测天气。
3.2 一杯热咖啡与混沌
热液体是受混沌法则支配的许多流体力学过程之一。以一杯简单的咖啡为例,我们怎样才能计算出一杯咖啡究竟会以怎样的速度冷却下来?如果咖啡只是热的,它的热量会在没有任何流体力学运动的情况下耗散,因此不会产生湍流。但是如果温度上升到咖啡开始沸腾,会发生什么?
如果你仔细观察过一杯热咖啡,会立即注意到在饮料表面有一条暗线勾勒出的土灰色漩涡区域。这些旋转的斑图被称为对流单元。它标志着热咖啡上升到表面,而稍微冷却的咖啡被引力拉向底部的区域。对流是一种常见的过程,当较热的空气或液体位于较冷的下层时就会发生。这就是咖啡杯中发生的情况:上面的咖啡因蒸发而冷却,随着冷却也变得更重,被重力拉下底部。同时,底部的咖啡中较热的部分上升到顶部以取代它。
漩涡可能很复杂。但最终我们能够知道这个系统会变成什么。随着热量的进一步消散,同时摩擦使移动的液体变慢,杯中咖啡的内部运动肯定会停止。洛伦兹在评论这一现象时曾说:"我们可能难以提前一分钟预测咖啡的温度,但提前一小时预测它应该没有什么困难。“
根据教科书上的对流模型,热的底部和冷的顶部之间的温度差控制着系统的流动。简单地说,热量向顶部移动,但并不干扰液体保持静止的趋势。
然而,当开始加热时可以观察到,随着液体变得更热,它的体积扩大,密度降低,使其轻到足以克服摩擦并向表面上升。但如果热量进一步增加,液体的行为会变得更加复杂。卷动的液体开始摇晃,为湍流的形成做准备。
因此,一个看似稳定的系统,当面对微小的变化时,如加热仅0.001度,就可以在几秒钟内从有序对流过渡到湍流混沌——即使这种系统是确定性的,它的最终结果可以预测。然而,在短期内,系统的确定性趋势必须向混沌让步,使得诸如“一杯咖啡的温度”这样简单的事情无法预测。这样的系统被称为遵循确定性的混沌,其行为原则上是可以被预测的,但“随着时间的推移”或在更小的“时间”尺度,其不可预知性会出现。
4.混沌斑图
自然界中的混沌斑图就在我们身边。这些斑图包括但不限于流体中的分形和湍流,螺旋形或者二维曼德布洛特集合形,或像洋葱中的嵌套层那样普遍的事物。
自然界中的混沌是一项迷人的研究。从最小的雪花到庞大的星系,它的每一点、每个声音和景象都在诉说着自己的故事。这不禁令人着迷,因为它有如此多的层次可以探索!从由不同材料组成的建筑结构(如砖或玻璃)内的音乐回声,一直到诸如包含后代遗传信息 DNA 的细胞等更小的结构,混沌无处不在。
大自然是一幅用秩序和混沌的图案编织的毯子。让我们探索其中的一些斑图。
4.1 洛伦兹系统:混沌理论中的蝴蝶效应和奇异吸引子
在洛伦兹观察到天气模式对初始条件的敏感依赖后,他对混沌背后的数学产生了浓厚的兴趣,并由此发现了著名的洛伦兹方程。1963年3月,洛伦兹写道,他想引入求解确定性非周期流和有限幅度对流(确定性混沌)的常微分方程。洛伦兹发现,当将傅立叶级数应用于瑞利的对流方程时,除了三个变量外,其他变量都趋于零。这三个变量表现出不规则的、明显的非周期效应。他利用这些变量构建了一个基于地球大气二维表示的简单模型。
他提出了一组对流微分方程,并将其简化到极致。尽管洛伦兹系统没有完全模拟对流,但它能够抽象出现实世界中对流的一个特征:热流体上升并向四处流动的循环运动过程。
洛伦兹方程如下:
dx/dt = X’ = σ(y − x)
dy/dt = Y’ = ρx − y − xz
dz/dt = Z’ = xy − βz
洛仑兹方程包含三个参数:σ, ρ, β。接下来,我们均假设这些参数都是正的。在下面所有的数值计算中,我们取 σ = 10.0, β = 8/3,ρ 是变量。这里 x、y、z 并不是指空间中的坐标。x代表平面上的对流翻转,y和z分别代表水平和垂直的温度变化。该模型的参数为σ,代表流体粘度与其热导率之比;ρ 代表大气平面顶部与底部的温差;β 代表平面的宽度与高度之比。
洛伦兹的电脑记录下三个变量的变化值:0-10-0;4-12-0;9-20-0;16-36-2;30-66-7;54-115-24;93-192-74。随着预设时间间隔的推移,这三个数字先上升后下降。洛伦兹用每组的 xyz 值作为坐标绘制数据图。这副图显示了当一个变量经历有限时间内的变化时,混沌系统如何随时间变化。过去对系统的传统预期是,它要么会稳定下来,进入一个稳态,速度和温度的变量将不再变化;要么可能会形成一个循环,进入一种周期性重复的行为模式。而这两者都没有在洛伦兹系统里出现。

洛伦兹系统
这幅图形成了一种无限复杂的感觉,同时包含了混沌和秩序。它总是在一定的范围内运转,但与此同时,它从不重复自己曾经出现过的状态。生成的混沌系统可预测地朝着相空间中的吸引子移动——但出现的不是点或简单的环,而是奇异吸引子。奇异吸引子是混沌系统在特定相空间中的一种表现,但吸引子也存在于许多非混沌的动力系统中。
它的形状看起来像个三维的双螺旋,看起来像一只蝴蝶。因此被称为蝴蝶效应。
洛伦兹吸引子(蝴蝶效应)微分方程在 Java 中的示例实现:
int i = 0;double x0, y0, z0, x1, y1, z1;double h = 0.01, a = 10.0, b = 28.0, c = 8.0 / 3.0;x0 = 0.1;y0 = 0;z0 = 0;for (i = 0; i < N; i++) {x1 = x0 + h * a * (y0 – x0);y1 = y0 + h * (x0 * (b – z0) – y0);z1 = z0 + h * (x0 * y0 – c * z0);x0 = x1;y0 = y1;z0 = z1;// Printing the coordinatesif (i > 100)System.out.println(i + ” ” + x0 + ” ” + y0 + ” ” + z0);}
洛伦兹微分方程组证明了混沌中隐藏着秩序。这种混沌本身并不能简化为随机性。混沌的核心终于可以被数学的诗意语言表达了。混沌背后的数学理论表明,宇宙是由复杂的系统控制的,这些系统同时产生了湍流和相干——无论是木星的大红斑还是物种种群。蝴蝶效应就是混沌的体现。
4.2 费根鲍姆常数和混沌理论
混沌的数学表示确立了非线性的重要性,这一特性支配着大多数自然系统,包括种群数量的增加。例如,如果1000只大象的群体每年净增10个成员,那么种群数量的增加可以在图表上表示为一条直线。然而,一群小鼠如果每年增加一倍的种群数量,将有一个非线性的增长模式——该图可以表示为一条上升的曲线。十年后,由于增长的非线性特征,两个小鼠群体(一个有22只小鼠,另一个有20只小鼠)之间的差异将膨胀到2000多只。因此,非线性增长模式常常导致动物种群规模混乱地上升和下降。
事实上,理解混沌理论最好的方法之一就是观察动物种群。假设方程 x_next = rx (1-x) 代表种群的增长。在这里,x_next 表示下一年的种群数量,x 表示现有年份的种群数量;r 表示增长率,(1-x)表示使增长保持在一定范围内的因素:当 x 增加时,(1-x) 下降。在这里,种群数量被表示为0到1之间的一个分数,其中0代表灭绝,1代表物种可能达到的最大种群数量。如果种群数量在一年内下降到某一水平以下,那么明年就有可能增加。但是,如果种群数量增长过快,物种内部对资源的竞争就会趋向于将其限制在一定范围内。
经过多次初始波动后,总体将达到平衡。当r值很小时,种群逐渐灭绝。对于较大的r值,总体可能收敛于单个值。对于更大的值,它可能在两个值之间波动,然后是四个值,以此类推。但对于更大的值,一切都变得不可预测。代表种群函数的线,最初是单一的,然后分裂成两个、四个...... 然后进入混沌。这种情况的种群数量-r曲线产生了有趣的结果。
当r在0和1之间时,种群最终灭绝。在 r = 1 到 r = 3 之间,种群数量收敛到单一值。在r = 3.2左右时,图分叉(分成两个),因为在r的这个值处,种群数量不收敛于单个值,而是在两个值之间波动。r值越大,分岔速度越快;在连续的周期翻倍之后,图像很快变得混沌。这意味着,对于r的相应值,种群数量在随机值之间不可预测地波动,从不表现出周期性行为。然而,仔细观察会发现,在混沌部分之间的某些点时,图会变得可预测。这些可以被称为“混沌中的秩序之窗”。在最初的混沌行为之后,混沌突然消失,留下一个稳定的三周期。然后继续加倍——6, 12, 24,再次进入混沌状态…...图中的混沌行为实际上是分形的。它展示了在植物和动物种群调节的简单模型中固有的非线性如何导致混沌的行为。
超过某一点,周期性就会让位给混沌,波动根本就不会稳定下来。图中的整个区域都被完全遮住了。如果你继续观察一个由这种最简单的非线性方程组支配的动物种群,你会发现,复杂性被隐藏为随机性。然而,复杂性并不意味着随机性。对于动物种群数量的每一个疯狂的、不可控的变化,我们观察到有一连串的事件年复一年地出现。即使参数在上升,这意味着非线性推动系统越来越难,但会突然出现一个具有固定周期的窗口:一个奇数周期,如3或7。种群数量变化的模式在3年或7年的周期中重复出现。然后,周期加倍的分叉以更快的速度重新开始,迅速通过3、6、12......或7、14、28......的周期,然后再次中断,重新进入混沌。
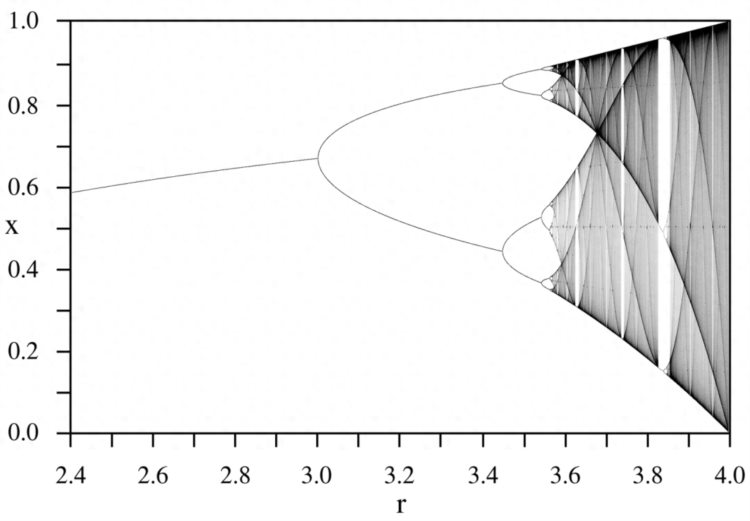
种群分岔图
放大后可以看到,上图中的混沌部分无休止地重复着同样的模式。分形是永无止境的。分形是无限复杂的斑图,在不同的尺度上具有自相似性。它们是通过在一个持续的反馈循环中不断重复一个简单的过程而产生的。从本质上讲,分形是一种永远重复的斑图,分形的每一部分,无论你如何放大,或缩小,它看起来都与整个图像非常相似。在递归的驱动下,分形是动态混沌系统的图像——它是混沌的图片。正如詹姆斯·格雷克(James Gleick)所说,"这是一种看待无限的方式"。
经过调查,数学家米歇尔·费根鲍姆(Mitchell Feigenbaum)发现,当他用每个分岔段的宽度除以下一个分岔段的宽度时,它们的比率会收敛到一个常数,被称为费根鲍姆常数,即4.6692016090。对于所有的分叉图,无论他使用什么函数,这个数字都是一样的。尺度是关键。费根鲍姆认为,(跨越不同范围的)尺度是理解湍流等复杂现象的关键。费根鲍姆提出了一种称为周期倍增的情况来描述规则动力学和混沌之间的转变。他的建议是基于1976年生物学家罗伯特·M·梅(Robert M. May)提出的 logistic 映射,梅在研究动物种群的繁荣与萧条模式时发现了分岔。
随着时间的推移,复杂性的规则也被证明是普遍的,并适用于所有的动力系统,不管它们的组成部分是什么。这种行为可以通过一个简单的系统观察到,比如水龙头滴水。最初,水会一滴一滴地落下。随着水流的加速,它会成对地滴落,以此类推,然后它遵循一种混沌的行为。这种类型的行为适用于无数的混沌系统——从滴水到异常复杂的曼德布洛特集合。混沌无处不在。
4.3 曼德布洛特集合和混沌理论
出生于波兰的法裔美国人伯努瓦·曼德布洛特(Benoit Mandelbrot)是一位对实用科学有广泛兴趣的博学者。现在人们对分形几何的兴趣很大部分是他的功劳。他展示了分形如何在数学和自然界中呈现。事实上,分形已经被用来描述经济、金融、股票市场、天文学和计算机科学的各种行为。他在分形几何学上的贡献为他赢得了“分形之父”的称号。
1961年,曼德布洛特在美国纽约州约克城高地托马斯·J·沃森研究中心担任研究科学家。作为一名尚未找到自己专业定位的年轻聪明学者,曼德布洛特正是那种IBM招聘时所渴求的特立独行的知识分子。招聘任务很简单:IBM参与了通过电话线传输计算机数据的工作,但一种白噪声不断干扰信息流,破坏信号。IBM希望曼德布洛特能对这个问题提供一个新的视角。
从孩提时代起,曼德布洛特就习惯在视觉层面思考问题,所以他没有使用现成的分析技术,而是本能地从白噪声产生的形状角度来研究它——这是IBM当今著名的数据可视化实践的早期形式。湍流的曲线图很快揭示了一个奇特的特征。无论图表的规模如何,无论它代表的是一天、一小时或一秒的数据,干扰的模式都惊人地相似。有一个更大的结构在起作用:一段时间的无误信号,紧接着就是一段时间的错误信号。曼德布洛特发现了误差爆发和清晰传输空间之间一致的几何关系。传输误差就像时间排列的康托集(Cantor set)。他将这种变化分为两种
