
古人云:“学然后知不足,教然后知因。”这个假期,有幸参加顺德区2022年“省级基础教育教研基地小学数学种子教师”培养活动,两场线上活动分别邀请了王永胜老师和陈静安教授给予我们专业指导。通过这次培训,让已经在教育岗位工作三年的我对教学、育人、专业发展都有了更深刻的认识,明白了只有不断学习前行,才能真正享受作为一名教师的诗与远方。
《探索活动:梯形的面积》
新学期我将任教五年级,因此对这一教学设计颇为关注。从新课标要求来看,梯形的面积属于图形与几何领域,新课标对图形与几何领域提出两个基本的素养要求:几何直观、空间观念。几何直观的素养达成是通过图表的手段建立“数与形”的联系,构建直观模型来解决问题。由此产生思考:如何通过面积的教学向学生进一步感悟度量的方法,并发展学生的量感和推理意识?王老师针对这些思考从新课标要求进行一一分析。
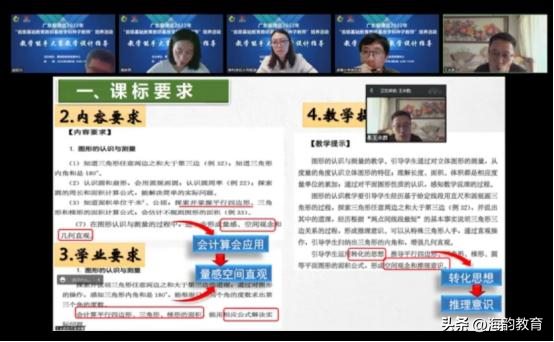
从结构来看,《梯形的面积》是学生已经学习了平行四边形,三角形面积公式的推导方法基础上进行,是学习经验的再利用,再生长。本课利用预习单回顾旧知,迁移学习经验,构建新旧之间的联系,并大胆让学生思考:“猜一猜,梯形的面积可能与什么有关?”
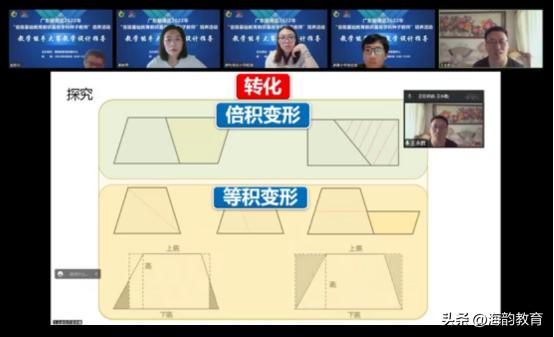
从教学内容来看,通过前面的复习,猜测,引导学生运用转化的思想,以小组合作探究的模式解决问题。学生在操作过程中运用剪、切、拼、折这样的等积变形,倍积变形方式,直观感悟梯形的面积是与什么图形有关,从而发展学生的空间观念,感受数学的美。这里学生出现的情况是多样的,老师这时抓住“梯形的面积是拼成的平行四边形面积的一半”这个结论,继续探索梯形面积的计算方法。
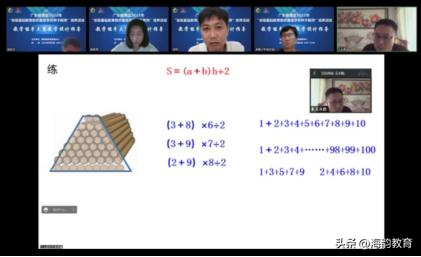
最让我印象深刻的,是巩固练习环节。对于计算木头根数这道题相信大家都不陌生,无论是常态课还是比赛课,都常常作为教学《梯形的面积》这一课的练习题。但是,我们往往在分析题目时,只是把这个物体的横截面看成梯形,上下木头的根数看成梯形的上底和下底,木头的层数就是梯形的高,再运用梯形的面积公式进行计算这就过了。但是,在王老师的分析中,这道题还是有很多值得深挖和思考的地方:
①继续在上、下加木头,计算面积。
②由1+2+3+4+5+6+7+8+9+10这样的数列计算也可以转化成梯形的面积,相当于最上面只有一根,最下面10根,数字的个数相当于梯形的高。
③根据②的规律思考高斯的问题:1+2+3+4+······+98+99+100。
④如果把②中的偶数都去掉,1+3+5+7+9 该怎么计算呢?2+4+6+8+10呢?在这个过程中让学生感悟“数形结合”的思想。
通过王老师的分析,让我深刻体会到,在日常教学中,巩固练习不在于多,不在于难,而是要善于挖掘里面的价值和内涵,既要帮助学生巩固新知,又要打通知识间的联系。
如果说王老师是让数学课上得更有味道,那陈教授则是让数学课上得更有依据。“天下难事必做于易,天下大事必作于细。”这是陈教授反复强调了一句话。凡事必由简至繁,而又化繁为简,同时在解决问题的过程中,时刻关注细节。此外,陈教授对于“新课标”的解读也是十分到位,从中也让我明白,只有在深入研读“新课标”要求的基础上再去审视教材,才能读懂教材编写的意图,把握教学的方向和目标,也更能关注学生的长远发展。
“惟保守也,故永旧;惟进取也,故日新。”纵观古今,我国的教育取得的发展离不开前人的不断研究与创新。作为新时代的教师更应该不断更新自己的知识,这样才能培养出来新时代的人才。
数学建模33讲 数学与缤纷的世界
¥89.9
购买
